«`html
Устойчивость в моделировании данных: общий подход с использованием теоремы о центральном пределе
Метод дистилляции модели — это способ создания интерпретируемых моделей машинного обучения с использованием более простой «ученической» модели для воспроизведения прогнозов сложной «учительской» модели. Однако, если производительность ученической модели значительно меняется с различными наборами обучающих данных, ее объяснения должны быть более надежными. Существующие методы стабилизации дистилляции включают в себя генерацию достаточного количества псевдо-данных, но эти методы часто адаптированы к конкретным типам ученических моделей. Для решения этой проблемы используются стратегии, такие как оценка стабильности критериев принятия решений в деревьях принятия решений или выбор признаков в линейных моделях. Эти подходы, хотя и полезны, ограничены зависимостью от конкретной структуры ученической модели.
Практические решения и ценность
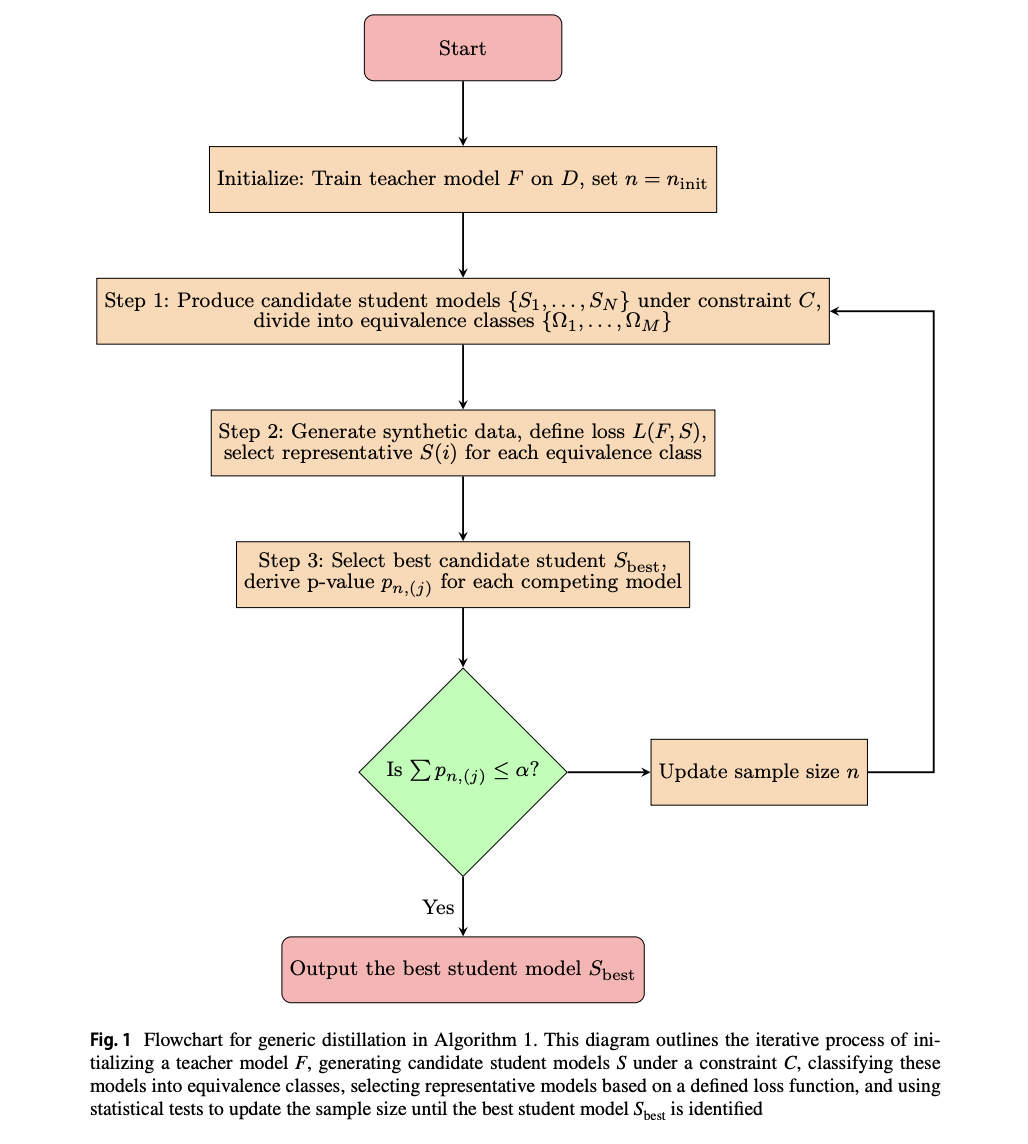
Исследователи из Университета Калифорнии в Беркли и Университета Пенсильвании предлагают общий метод стабилизации дистилляции модели с использованием подхода теоремы о центральном пределе. Их рамочная модель начинается с нескольких кандидатов-учеников, оценивая, насколько хорошо они соответствуют учительской модели. Они используют множество тестовых рамок для определения необходимого объема выборки для последовательных результатов на разных псевдовыборках. Этот метод демонстрируется на деревьях принятия решений, списках правил падения и моделях символьной регрессии, с применением на наборах данных о маммографических опухолях и раке груди. Исследование также включает теоретический анализ с использованием процесса Маркова и чувствительного анализа факторов, таких как сложность модели и объем выборки.
Исследование представляет надежный подход к стабильной дистилляции модели путем получения асимптотических свойств среднего убытка на основе теоремы о центральном пределе. Они используют эту структуру для определения вероятности выбора фиксированной структуры модели на разных псевдовыборках и расчета необходимого объема выборки для контроля этой вероятности. Кроме того, исследователи реализуют несколько процедур множественного тестирования, чтобы учесть конкурирующие модели и обеспечить стабильность в выборе модели. Метод включает в себя генерацию синтетических данных, выбор лучшей ученической модели из кандидатских структур и итеративное корректирование объема выборки до тех пор, пока не будет выявлена значительная модель.
Исследователи специально затрагивают три понятные ученические модели — деревья принятия решений, списки правил падения и символьную регрессию — демонстрируя их применимость в обеспечении интерпретируемых и стабильных модельных объяснений. Используя методы Монте-Карло, байесовскую выборку и генетическое программирование, мы генерируем разнообразные кандидатские модели и классифицируем их в эквивалентные классы на основе их структур. Данный подход контрастирует с методами ансамблей, фокусируясь на стабильности и воспроизводимости в выборе модели, обеспечивая последовательные объяснения для учительской модели на различных выборках данных.
Эксперименты на двух наборах данных с использованием общего алгоритма дистилляции модели, сосредоточенные на чувствительном анализе ключевых факторов. Настройка включает бинарную классификацию с потерей перекрестной энтропии, фиксированную учительскую модель случайного леса и генерацию синтетических данных. Эксперименты включают 100 запусков с различными сидами. Гиперпараметры включают уровень значимости (альфа) 0,05, начальный объем выборки 1000 и максимальную длину 100 000. Метрики оценки охватывают стабильность интерпретации и верность ученической модели. Результаты показывают, что стабилизация улучшает согласованность структуры модели, особенно в выборе признаков. Чувствительный анализ показывает, что увеличение кандидатских моделей и объема выборки улучшает стабильность, в то время как сложные модели требуют более крупных выборок.
Исследование представляет стабильный метод дистилляции модели с использованием проверки гипотез и тестовых статистик на основе теоремы о центральном пределе. Подход обеспечивает генерацию достаточного количества псевдо-данных для выбора надежной структуры ученической модели из кандидатов. Теоретический анализ формулирует проблему как процесс Маркова, предоставляя границы сложности стабилизации с комплексными моделями. Эмпирические результаты подтверждают эффективность метода и подчеркивают сложность различения сложных моделей без обширных псевдо-данных. В дальнейшем работе предполагается улучшение теоретического анализа с учетом границ Берри-Эссена и классов Донскера, учет неопределенности учительской модели и изучение альтернативных процедур множественного тестирования.
Проверьте статью и GitHub. Вся заслуга за это исследование принадлежит исследователям этого проекта. Также не забудьте подписаться на наш Твиттер и присоединиться к нашему Телеграм-каналу и группе в LinkedIn. Если вам нравится наша работа, вам понравится наша новостная рассылка.
Не забудьте присоединиться к нашему сообществу в Reddit по ИИ.
Найдите предстоящие вебинары по ИИ здесь
Опубликовано на MarkTechPost.

