«`html
Решения для улучшения путей сокращения тензоров с использованием модифицированного жадного алгоритма с улучшенной функцией стоимости
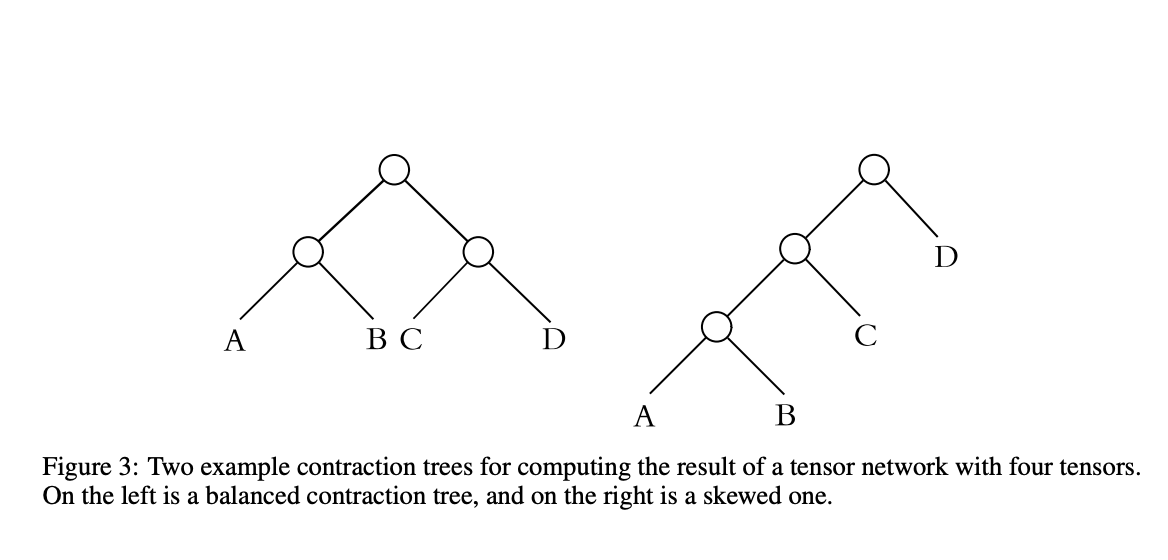
Тензорные противоречия используются для решения проблем, связанных с различными областями исследований, включая подсчет моделей, квантовые цепи, графовые проблемы и машинное обучение. Для минимизации вычислительных затрат важно найти порядок противоречий. Результат вычисления произведения последовательности матриц A, B и C всегда будет одинаковым, но вычислительные затраты будут различными в зависимости от размеров матриц. Более того, стоимость сокращения для тензорных сетей увеличивается с увеличением количества тензоров. Путь, используемый для определения того, какие два тензора сокращаются друг с другом, важен для улучшения времени вычислений.
Практические решения и ценность
Ранее работы были сосредоточены на поиске эффективных путей сокращения тензорных гиперсетей. Для вычисления путей сокращения тензоров одним из существующих методов является использование имитации отжига и генетического алгоритма, который превосходит стандартный жадный подход для более маленьких сетей. Второй метод — это разложение графа, в котором используются методы Line-Graph (LG) и Factor-Tree (FT). LG использует структурированный анализ графа для нахождения порядка сокращения, в то время как FT используется в предварительной обработке для работы с тензорами высокого ранга. Третий метод, в котором объединяются обучение с подкреплением (RL) и графовые нейронные сети (GNN), используется для нахождения эффективного пути и включает реальные и синтетические квантовые цепи.
Команда исследователей предложила новый метод для улучшения путей сокращения тензоров с использованием модифицированного стандартного жадного алгоритма с улучшенной функцией стоимости. Этот метод превосходит реализации жадного алгоритма от Optimized Einsum (opt_einsum) и, в некоторых случаях, превосходит методы, такие как разбиение гиперграфа в сочетании с жадным подходом.
Исследователи использовали SGA в opt_einsum для эффективного нахождения путей сокращения для большого количества тензоров. Процесс вычисления путей сокращения состоит из трех фаз:
- Вычисление покомпонентного произведения тензоров с одинаковым набором индексов.
- Сокращение оставшихся тензоров до тех пор, пока все индексы сокращения не будут использованы, выбирая наименьшую стоимость на каждом шаге.
- Вычисление внешних произведений путем выбора пары, минимизирующей сумму размеров входных данных на каждом шаге.
Кроме того, модифицированный жадный алгоритм использует функции стоимости в качестве параметров, в отличие от SGA, который использует только одну функцию стоимости. Затем различные функции стоимости используются во время выполнения, и наиболее подходящая функция стоимости выбирается для генерации дальнейших путей сокращения.
В заключение, исследователи предложили новый подход для улучшения путей сокращения тензоров с использованием модифицированного стандартного жадного алгоритма. Подход с множественными функциями стоимости используется, где каждая функция стоимости рассчитывается для каждого примера проблемы, и лучшая функция стоимости выбирается для вычисления путей сокращения. По сравнению со стандартными жадными и случайными жадными алгоритмами от opt_einsum, а также жадным алгоритмом и методом разбиения гиперграфа, предложенный метод может быстро находить эффективные пути сокращения в меньшее время и решать сложные проблемы, которые другие методы не могут решить.
Подробнее ознакомьтесь с статьей. Вся заслуга за это исследование принадлежит исследователям этого проекта. Также не забудьте подписаться на наш Twitter. Присоединяйтесь к нашему каналу в Telegram, Discord и группе в LinkedIn.
Если вам нравится наша работа, вам понравится наша рассылка.
Не забудьте присоединиться к нашему сообществу в Reddit с более чем 42 тысячами подписчиков.
Источник: MarkTechPost
«`



















