«`html
Улучшение математического мышления в LLMs: Интеграция метода Монте-Карло с самосовершенствованием
Современные достижения в области искусственного интеллекта, такие как LLMs, такие как GPT-4 и LLaMA, значительно улучшили обработку естественного языка. Эти модели, обладающие миллиардами параметров, отлично справляются с пониманием и генерацией языка, позволяя новые возможности в сложных задачах, таких как решение математических проблем, системы рекомендаций и генерация молекул.
Применение в реальном мире
Однако LLMs испытывают трудности с задачами, требующими точного рассуждения, часто допуская ошибки или «галлюцинации», особенно в математических контекстах. Методы, такие как Self-Refine, могут смягчить эту проблему, но такие неточности все равно могут привести к вводящим в заблуждение или неправильным результатам в сложных прикладных задачах.
Практические решения
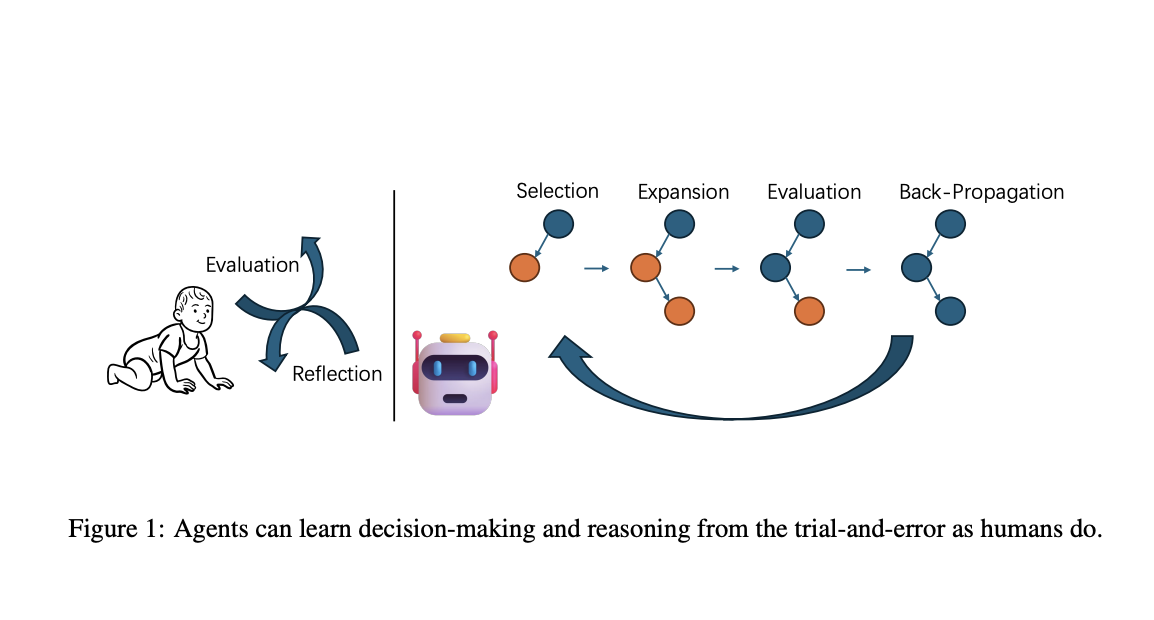
Исследователи из Университета Фудан и Шанхайской лаборатории искусственного интеллекта разработали алгоритм MCT Self-Refine (MCTSr), объединяющий LLMs с методом Монте-Карло для улучшения математического рассуждения. Это интеграция использует систематическое исследование Монте-Карло и возможности самосовершенствования LLMs для улучшения принятия решений в сложных задачах.
Метод Монте-Карло был успешно применен в различных областях для решения сложных проблем, от оптимизации многопользовательского поиска пути до решения проблемы составления расписания поездов и различных проблем SAT. Недавние инновации включают интеграцию метода Монте-Карло с нейронными сетями, информированными физикой, для динамических задач робототехники.
Алгоритм MCTSr значительно улучшает качество ответов в сложных задачах рассуждения, интегрируя метод Монте-Карло с большими языковыми моделями. Он итеративно улучшает ответы через самосовершенствование и оценивает их с помощью механизмов самооценки, обеспечивая баланс исследования и эксплуатации для оптимизации принятия решений.
Для оценки эффективности алгоритма MCTSr модель LLaMA3-8B была усовершенствована с помощью MCTSr и протестирована на различных математических бенчмарках. Результаты показали четкую корреляцию между увеличением количества прогонов MCTSr и более высокими показателями успеха, особенно в более простых задачах. Однако производительность стабилизировалась на более сложных наборах данных, показывая ограничения текущего подхода.
Алгоритм MCTSr показал значительный потенциал в улучшении способности LLMs решать сложные математические задачи. Экспериментальные оценки на различных наборах данных, включая сложные олимпиадные задачи, подчеркивают существенные улучшения в показателях успешности решения проблем. В настоящее время фокус исследований сосредоточен на математических приложениях, но широкий потенциал MCTSr в областях, таких как оптимизация черного ящика и самонаправленное выравнивание для LLMs, предполагает многообещающие перспективы для будущих исследований.
Подробнее ознакомьтесь с исследованием. Вся заслуга за это исследование принадлежит исследователям этого проекта. Также не забудьте подписаться на наш Twitter.
Присоединяйтесь к нашему Telegram-каналу и группе в LinkedIn.
Если вам нравится наша работа, вам понравится наша рассылка.
Не забудьте присоединиться к нашему SubReddit с более чем 44 тысячами подписчиков.
Источник: MarkTechPost.
«`




















