«`html
Колмогоров-Арнольдовские сети (KAN) как альтернатива традиционным многослойным персептронам (MLP)
Колмогоров-Арнольдовские сети (KAN) представляют собой многообещающую альтернативу традиционным многослойным персептронам (MLP). Используя теорему представления Колмогорова-Арнольда, эти сети используют нейроны, выполняющие простые операции сложения. Однако текущая реализация KAN представляет определенные вызовы в практических приложениях. Исследователи в настоящее время изучают возможность определения альтернативных многомерных функций для нейронов KAN, которые могли бы предложить улучшенную практическую ценность в различных бенчмарках, связанных с задачами машинного обучения.
Потенциал KAN в различных областях
Исследования выявили потенциал KAN в различных областях, таких как компьютерное зрение, анализ временных рядов и поиск квантовой архитектуры. Некоторые исследования показывают, что KAN может превзойти MLP в задачах подгонки данных и решении уравнений в частных производных, используя при этом меньшее количество параметров. Однако некоторые исследования вызывают опасения относительно устойчивости KAN к шуму и их производительности по сравнению с MLP. Также исследуются вариации и улучшения стандартной архитектуры KAN, такие как графовые конструкции, сверточные KAN и трансформаторные KAN для решения проблем. Кроме того, исследуются альтернативные функции активации, такие как вейвлеты, радиальные базисные функции и синусоидальные функции, для улучшения эффективности KAN. Несмотря на эти работы, существует потребность в дальнейших улучшениях для повышения производительности KAN.
Новый подход к улучшению производительности KAN
Исследователь из Центра исследований прикладных интеллектуальных систем Университета Халмстад, Швеция, предложил новый подход для улучшения производительности Kolmogorov-Arnold Networks (KAN). Этот метод направлен на определение оптимальной многомерной функции для нейронов KAN в различных задачах классификации машинного обучения. Традиционное использование сложения в качестве функции на уровне узла часто является неидеальным, особенно для высокомерных наборов данных с несколькими признаками. Это может привести к тому, что входные данные превысят эффективный диапазон последующих функций активации, что приведет к нестабильности обучения и снижению обобщающей производительности. Для решения этой проблемы исследователь предлагает использовать среднее вместо суммы в качестве функции узла.
Эксперименты и результаты
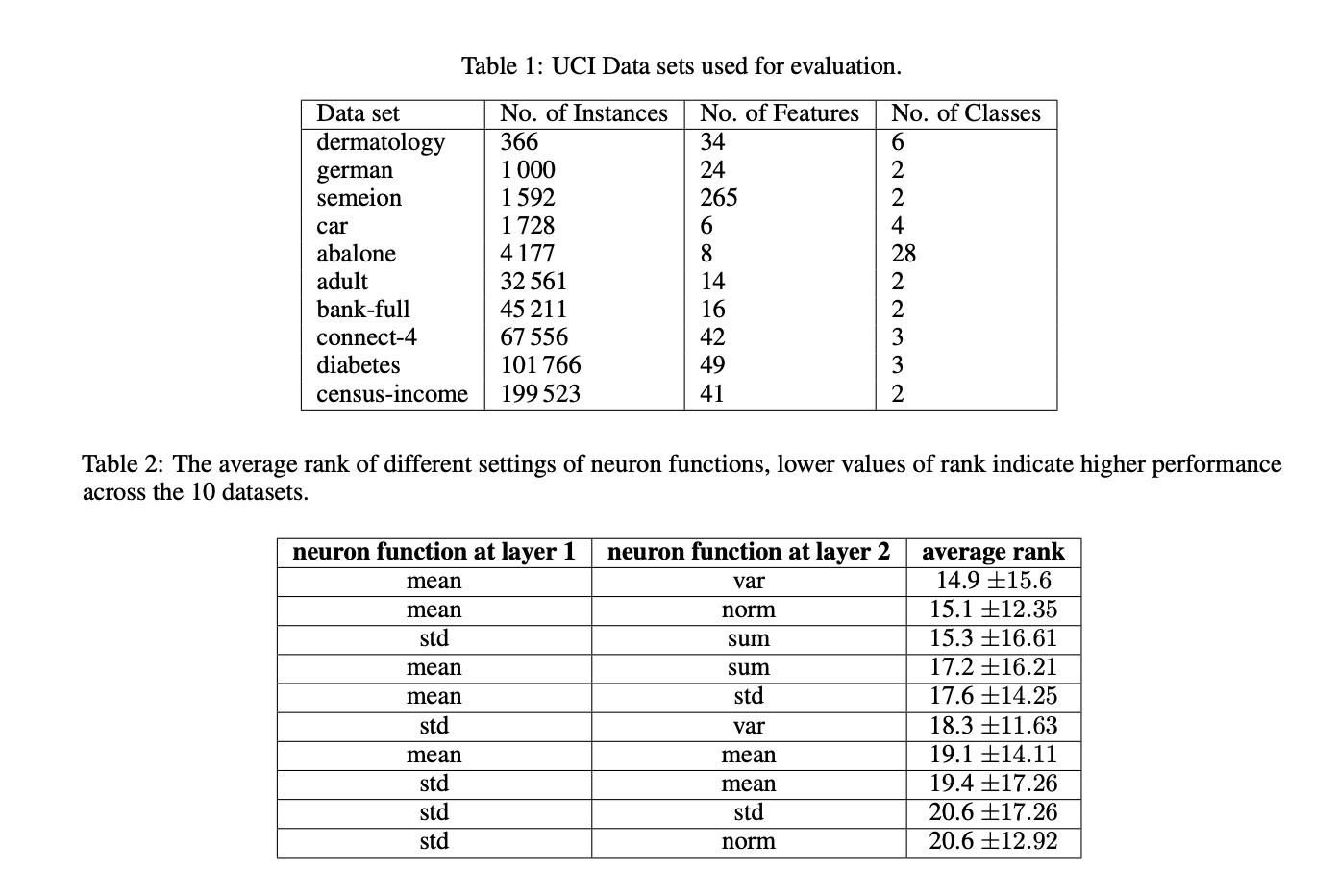
Для оценки предложенных модификаций KAN используются 10 популярных наборов данных из репозитория базы данных машинного обучения UCI, охватывающих различные области и различные размеры. Эти наборы данных разделены на обучающие (60%), валидационные (20%) и тестовые (20%) части. Применяется стандартизированный метод предварительной обработки для всех наборов данных, включая кодирование категориальных признаков, восстановление пропущенных значений и случайную перестановку экземпляров. Модели обучаются в течение 2000 итераций с использованием оптимизатора Adam с коэффициентом обучения 0.01 и размером пакета 32. Точность модели на тестовом наборе служит основной метрикой оценки. Количество параметров управляется путем установки сетки в 3 и использования параметров по умолчанию для моделей KAN.
Результаты подтверждают гипотезу о том, что использование функции среднего в нейронах KAN эффективнее, чем традиционная функция суммирования. Это улучшение обусловлено способностью среднего сохранять входные значения в оптимальном диапазоне функции активации сплайнов, который составляет [-1.0, +1.0]. Стандартные KAN сталкивались с трудностями в поддержании значений в этом диапазоне в промежуточных слоях при увеличении количества признаков. Однако применение функции среднего в нейронах приводит к улучшению производительности, поддерживая значения в желаемом диапазоне на наборах данных с 20 или более признаками. Для наборов данных с меньшим количеством признаков значения оставались в диапазоне более чем 99,0% времени, за исключением набора данных ‘abalone’, где уровень соблюдения был немного ниже и составил 96,51%.
Этот подход к улучшению производительности KAN представляет собой важное изменение в архитектуре KAN, заменяя традиционное сложение в нейронах KAN на функцию усреднения. Экспериментальные результаты показывают, что эти изменения приводят к более стабильным процессам обучения и поддерживают входные данные в эффективном диапазоне функций активации. Это улучшение архитектуры KAN решает ранее возникшие проблемы, связанные с диапазоном входных данных и стабильностью обучения. В будущем эта работа предлагает многообещающее направление для будущих реализаций KAN, потенциально улучшая их производительность и применимость в различных задачах машинного обучения.
Проверьте статью. Вся заслуга за это исследование принадлежит исследователям этого проекта. Также не забудьте подписаться на наш Twitter и присоединиться к нашему каналу в Telegram и группе в LinkedIn. Если вам нравится наша работа, вам понравится наш новостной бюллетень.
Не забудьте присоединиться к нашему подразделению по машинному обучению с 47 тыс. подписчиков.
Найдите предстоящие вебинары по ИИ здесь.
Arcee AI выпустила DistillKit: открытый инструмент для моделирования, превращающий процесс дистилляции моделей в эффективные, высокопроизводительные малые языковые модели
Пост Колмогоров-Арнольдова теорема вновь рассмотрена: почему функции усреднения работают лучше на MarkTechPost.
«`




















