«`html
Большие языковые модели (LLM) и их метакогнитивные способности
Большие языковые модели (LLM) продемонстрировали впечатляющие способности к рассуждению в различных областях. Но обладают ли они также метакогнитивными знаниями – пониманием своих мыслительных процессов? Этот увлекательный вопрос исследуется в новой статье, которая рассматривает метакогнитивные способности LLM, в частности в контексте решения математических задач. Команда исследователей из Mila, Университета Монреаля, Принстонского университета, Кембриджского университета и Google DeepMind разработала инновационный подход для извлечения и использования неявных знаний LLM о математических навыках и концепциях с обнадеживающими результатами для улучшения математического рассуждения.
Практические решения и ценность
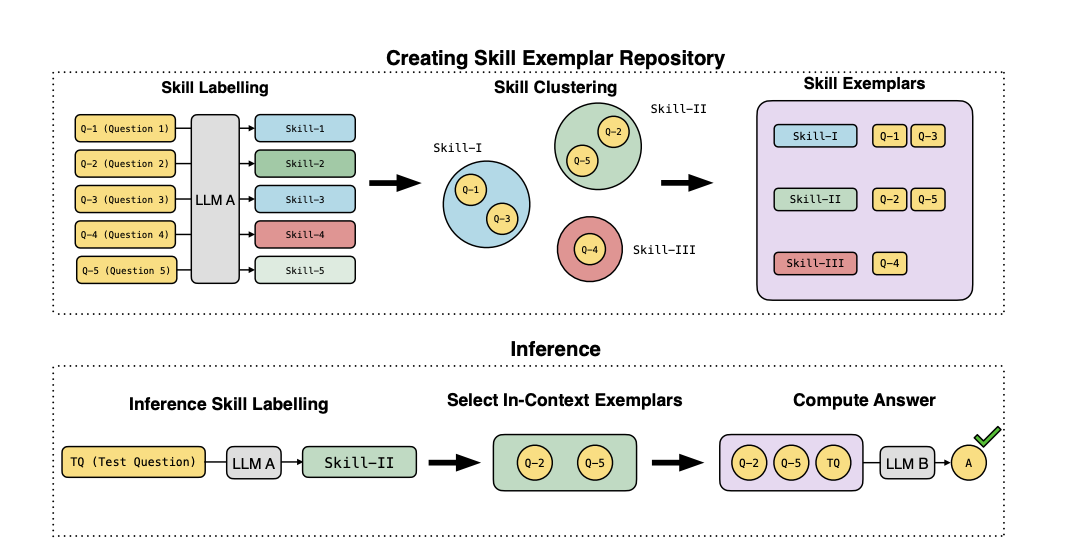
Текущие методы улучшения производительности LLM при решении математических задач часто полагаются на общие методики подсказок, такие как цепочка рассуждений. Хотя эти подходы эффективны, они не используют потенциальных метакогнитивных знаний моделей. Исследователи предлагают новый метод для извлечения скрытого понимания математических навыков LLM. Их подход включает использование мощной LLM, такой как GPT-4, для присвоения точных меток навыков математическим вопросам, а затем семантическую кластеризацию для получения более широких категорий навыков. Это приводит к созданию «Репозитория образцов навыков» – отобранного набора вопросов с толковыми метками навыков.
Ключевым инновационным моментом является использование этого репозитория во время вывода на новые математические задачи. При предъявлении вопроса LLM сначала просят определить наиболее релевантный навык из репозитория. Затем предоставляют образцы вопросов/ответов, связанных с этим навыком, в качестве примеров в контексте перед попыткой решения. Этот подход на основе навыков был оценен на сложных наборах данных, таких как GSM8K и MATH, охватывающих различные математические трудности. На наборе данных MATH он достиг впечатляющего улучшения на 11,6% по сравнению со стандартной цепочкой рассуждений. Метод также повысил производительность при интеграции с языковыми моделями, поддерживаемыми программой (PAL), которые генерируют кодовые решения.
Исследователи продемонстрировали, что извлеченные метакогнитивные знания мощной модели, такой как GPT-4, эффективно передаются для улучшения производительности более слабых LLM. Подход также показал сильную обобщаемость, улучшая результаты при применении к нескольким другим наборам данных математических задач, выходящим за пределы тех, которые использовались для создания репозитория навыков. Это исследование предлагает убедительные доказательства того, что LLM обладают существенными метакогнитивными знаниями о решении математических задач. Разработав методы извлечения и операционализации этих знаний, исследователи открыли увлекательные новые возможности для улучшения математического рассуждения LLM.
Преимущества подхода на основе навыков
Подход на основе навыков предоставляет несколько ключевых преимуществ: он позволяет использовать более целевые и актуальные примеры в контексте, может быть легко интегрирован с существующими методиками подсказок и демонстрирует сильную переносимость между моделями и наборами данных. Хотя есть место для улучшения, особенно в обработке задач, требующих нескольких навыков, эта работа представляет собой значительный шаг к более сложному математическому рассуждению в системах ИИ. Вне математики представленная методология может быть адаптирована для выявления и использования метакогнитивных знаний в других областях. Таким образом, это исследование продвигает наше понимание когнитивных процессов LLM и указывает на многообещающие новые направления для улучшения их общих возможностей через метакогнитивное стимулирование.
Проверьте статью. Вся заслуга за это исследование принадлежит исследователям этого проекта. Также не забудьте подписаться на нас в Twitter и LinkedIn. Присоединяйтесь к нашему Telegram-каналу.
«`



















