«`html
Генерализация градиентного спуска в перепараметризованных сетях ReLU: Виды минимальной стабильности и большие скорости обучения
Искусственные нейронные сети, обученные методом градиентного спуска, эффективно работают даже в перепараметризованных сценариях с случайной инициализацией весов, часто находя глобальные оптимальные решения, несмотря на не выпуклую природу проблемы. Эти решения, достигающие нулевую ошибку обучения, удивительно часто не переобучаются, что известно как «добросовестное переобучение». Однако для сетей ReLU интерполяционные решения могут привести к переобучению. Более того, лучшие решения обычно не интерполируют данные в сценариях с шумными данными. Практическое обучение часто прекращается до достижения полной интерполяции, чтобы избежать попадания в нестабильные области или решений с высокой чувствительностью к выбросам.
Практические решения и ценность
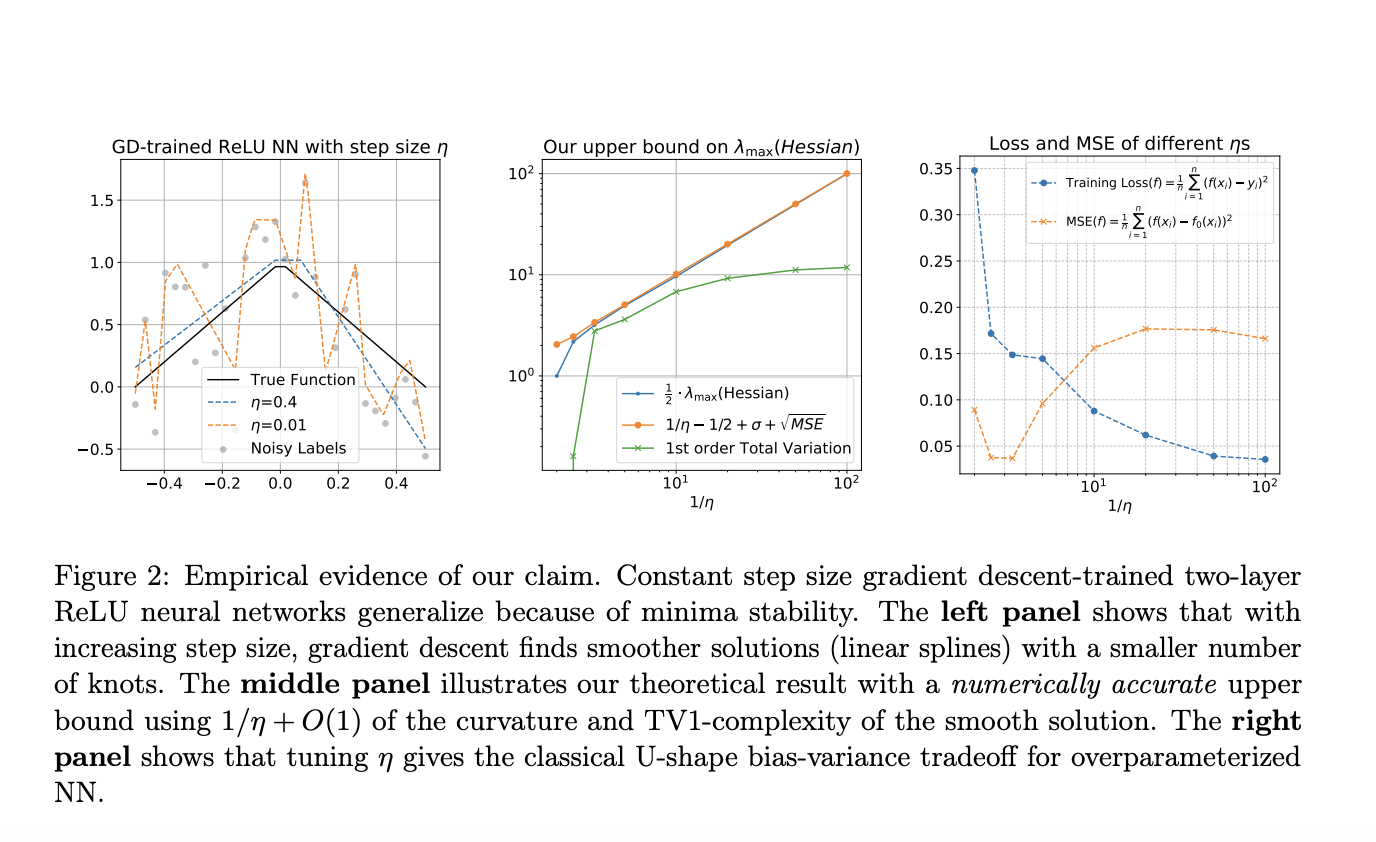
Исследователи из UC Santa Barbara, Technion и UC San Diego изучают обобщение двухслойных нейронных сетей ReLU в непараметрической регрессии 1D с шумными метками. Они представляют новую теорию, показывающую, что градиентный спуск с фиксированным темпом обучения сходится к локальным минимумам, представляющим собой гладкие, редко линейные функции. Эти решения, которые не интерполируют, избегают переобучения и достигают практически оптимального среднеквадратического отклонения (MSE). Анализ показывает, что большие темпы обучения индуцируют неявную разреженность и что сети ReLU могут обобщаться хорошо даже без явной регуляризации или ранней остановки. Эта теория выходит за рамки традиционных ядерных и интерполяционных фреймворков.
Ȧ в перепараметризованных нейронных сетях большинство исследований сосредоточено на обобщении в интерполяционном режиме и добросовестном переобучении. Обычно для этого требуется явная регуляризация или ранняя остановка для работы с шумными метками. Однако недавние исследования показывают, что градиентный спуск с большим темпом обучения может достигать разреженных, гладких функций, которые хорошо обобщаются, даже без явной регуляризации. Этот подход расходится с традиционными теориями, полагающимися на интерполяцию, демонстрируя, что градиентный спуск индуцирует неявное отклонение, похожее на L1-регуляризацию. Также проведенные исследования связаны с гипотезой о том, что «плоские локальные минимумы лучше обобщаются» и предоставляют информацию о достижении оптимальных коэффициентов в непараметрической регрессии без уменьшения весов.
Исследование адресует настройку и обозначение для изучения обобщения в двухслойных нейронных сетях ReLU. Модель обучается с использованием градиентного спуска на наборе данных с шумными метками, сфокусированных на проблемах регрессии. Ключевые концепции включают в себя стабильные локальные минимумы, которые дважды дифференцируемы и находятся на определенном расстоянии от глобального минимума. Исследование также исследует режим «Границы стабильности», где крупнейшее собственное значение гессиана достигает критического значения, связанного с темпом обучения. Для непараметрической регрессии целевая функция принадлежит классу ограниченного варьирования. Анализ демонстрирует, что градиентный спуск не может найти стабильные интерполяционные решения в шумных настройках, что приводит к более гладким, не интерполирующим функциям.
Основные результаты исследования исследуют стабильные решения для градиентного спуска (GD) на двухслойных нейронных сетях ReLU по трем аспектам. Во-первых, оно изучает неявное отклонение стабильных решений в функциональном пространстве при больших темпах обучения, показывая, что они по своей сути гладкие и простые. Во-вторых, извлекает обобщенные ограничения для этих решений в настройках непараметрической регрессии без распределения, демонстрируя, что они избегают переобучения. Наконец, анализ демонстрирует, что GD достигает оптимальных коэффициентов для оценки функций ограниченного варьирования в определенных интервалах, подтверждая эффективную производительность обобщения решений GD с большим темпом обучения, даже в шумных средах.
В заключение, исследование исследует, как двухслойные нейронные сети ReLU, обученные градиентным спуском, обобщаются через понимание стабильности минимумов и явления Границы стабильности. Оно сосредотачивается на невариативных входах с шумными метками и показывает, что градиентный спуск с типичным темпом обучения не может интерполировать данные. Исследование демонстрирует, что локальная гладкость функции обучения подразумевает ограничение общей вариации первого порядка на функцию нейронной сети, что приводит к исчезающему зазору обобщения в строгой поддержке данных. Кроме того, эти стабильные решения достигают практически оптимальных коэффициентов для оценки сплайнов первого порядка в переменном варьировании при мягком предположении. Симуляции подтверждают результаты, показывая, что обучение с большим темпом обучения ведет к разреженным линейным сплайнам.
Как можно применить ИИ-решения?
Если вы хотите, чтобы ваша компания развивалась с помощью искусственного интеллекта (ИИ) и оставалась в числе лидеров, грамотно используйте Generalization of Gradient Descent in Over-Parameterized ReLU Networks: Insights from Minima Stability and Large Learning Rates.
Проанализируйте, как ИИ может изменить вашу работу. Определите, где возможно применение автоматизации: найдите моменты, когда ваши клиенты могут извлечь выгоду из AI.
Определитесь какие ключевые показатели эффективности (KPI): вы хотите улучшить с помощью ИИ.
Подберите подходящее решение, сейчас очень много вариантов ИИ. Внедряйте ИИ-решения постепенно: начните с малого проекта, анализируйте результаты и KPI.
На полученных данных и опыте расширяйте автоматизацию.
Если вам нужны советы по внедрению ИИ, пишите нам на https://t.me/itinai. Следите за новостями о ИИ в нашем Телеграм-канале t.me/itinainews или в Twitter @itinairu45358
Попробуйте AI Sales Bot https://itinai.ru/aisales. Этот AI ассистент в продажах помогает отвечать на вопросы клиентов, генерировать контент для отдела продаж, снижать нагрузку на первую линию.
Узнайте, как ИИ может изменить ваши процессы с решениями от AI Lab itinai.ru. Будущее уже здесь!
Источник: MarkTechPost
«`
Hope this helps! Let me know if you need further assistance.





















