«`html
Научные открытия и искусственный интеллект: новые возможности
Наука стремится к открытию кратких и понятных формул, соответствующих теории и экспериментальным данным. Традиционно ученые получали естественные законы путем манипуляции уравнениями и экспериментальной проверки, но этот подход может быть неэффективным. Научный метод продвинул наше понимание, но темп открытий и их экономическое воздействие замедлились. Это замедление частично связано с исчерпанием легко доступных научных идей. Для решения этой проблемы необходимо интегрировать фоновые знания с экспериментальными данными для открытия сложных естественных законов. Недавние прорывы в методах глобальной оптимизации, обусловленные улучшением вычислительной мощности и алгоритмов, предлагают многообещающие инструменты для научных открытий.
Моделирование и оптимизация для научных открытий
Исследователи из Imperial College Business School, Samsung AI и IBM предлагают решение для научных открытий, моделируя аксиомы и законы в виде полиномов. Используя бинарные переменные и логические ограничения, они решают задачи оптимизации полиномов с помощью целочисленной линейной или полудопустимой оптимизации, проверенной сертификатами Positivstellensatz. Их метод может вывести хорошо известные законы, такие как Закон Кеплера и уравнение радиационной гравитационной волновой мощности, из гипотез и данных. Этот подход обеспечивает согласованность с фоновой теорией и экспериментальными данными, предоставляя формальные доказательства. В отличие от методов глубокого обучения, которые могут производить непроверяемые результаты, их техника гарантирует масштабное и надежное открытие новых научных законов.
Интеграция данных и теории для формулирования гипотез
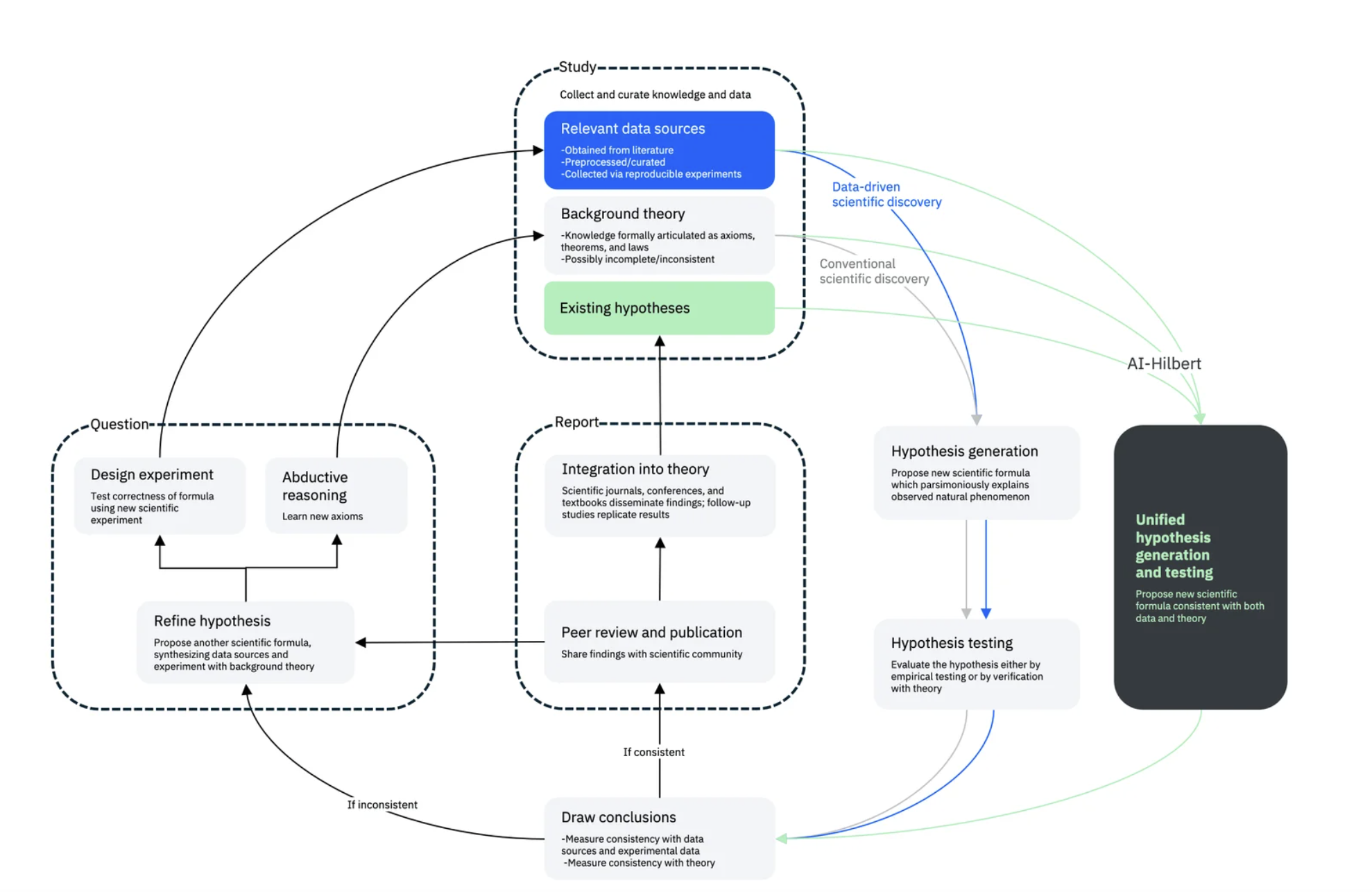
AI-Hilbert — это парадигма для научных открытий, которая идентифицирует полиномиальные законы, согласующиеся с экспериментальными данными и фоновой базой знаний о полиномиальных равенствах и неравенствах. Вдохновленная работой Давида Гильберта о связи сумм квадратов и неотрицательных полиномов, AI-Hilbert гарантирует, что обнаруженные законы аксиоматически правильны с учетом фоновой теории. В случаях, когда фоновая теория несогласована, подход идентифицирует источники несогласованности через лучший подмножественный выбор, определяя гипотезы, лучше всего объясняющие данные. Этот методологический подход отличается от текущих данных-приводимых подходов, которые производят ложные результаты в условиях ограниченных данных и не могут различать между допустимыми и недопустимыми открытиями или объяснить их происхождение.
Использование ИИ для оптимизации процессов
Исследование вводит инновационный метод для научных открытий, интегрирующий реальную алгебраическую геометрию и смешанную целочисленную оптимизацию для вывода новых научных законов из неполных аксиом и шумных данных. В отличие от традиционных методов, полагающихся исключительно на теорию или данные, этот подход объединяет их, обеспечивая открытия в условиях ограниченных данных и ограниченной теории. AI-Hilbert выявляет неявные полиномиальные взаимосвязи между переменными, предлагая преимущества в обработке неявных представлений, распространенных в науке. Будущие направления включают расширение рамок на не-полиномиальные контексты, автоматизацию настройки гиперпараметров и улучшение масштабируемости путем оптимизации основных вычислительных техник.
Попробуйте AI Sales Bot — это ИИ ассистент в продажах, помогающий отвечать на вопросы клиентов, генерировать контент для отдела продаж, снижать нагрузку на первую линию.
Узнайте, как ИИ может изменить ваши процессы с решениями от AI Lab itinai.ru — будущее уже здесь!
«`



















