«`html
Решение для моделирования нелинейных динамических систем
Моделирование нелинейных динамических систем на основе наблюдаемых данных остается значительной проблемой в различных областях, таких как динамика жидкостей, климатология и механическая инженерия. Традиционные методы линейной аппроксимации часто неспособны уловить сложное поведение этих систем, что приводит к неточным прогнозам и неэффективным стратегиям управления. Решение этой проблемы крайне важно для развития нашей способности анализировать, прогнозировать и управлять сложными явлениями в естественных и созданных человеком системах.
Текущие подходы и их ограничения
Текущие подходы, в частности, динамическое разложение моды (DMD) и расширенное динамическое разложение моды (EDMD), пытаются линеаризовать нелинейные системы путем приближения оператора Купмана. Хотя эти методики имели успех в определенных условиях, они обладают существенными ограничениями при применении к общим нелинейным системам. Их зависимость от строгих предположений часто приводит к моделям, которые переобучаются на обучающих данных и не могут эффективно обобщаться на новые сценарии. Кроме того, эти методы могут создавать высокоразмерные модели, требующие значительных вычислительных ресурсов и затрудняющие интерпретацию, что делает их непрактичными для прикладных систем и систем с ограниченными вычислительными ресурсами.
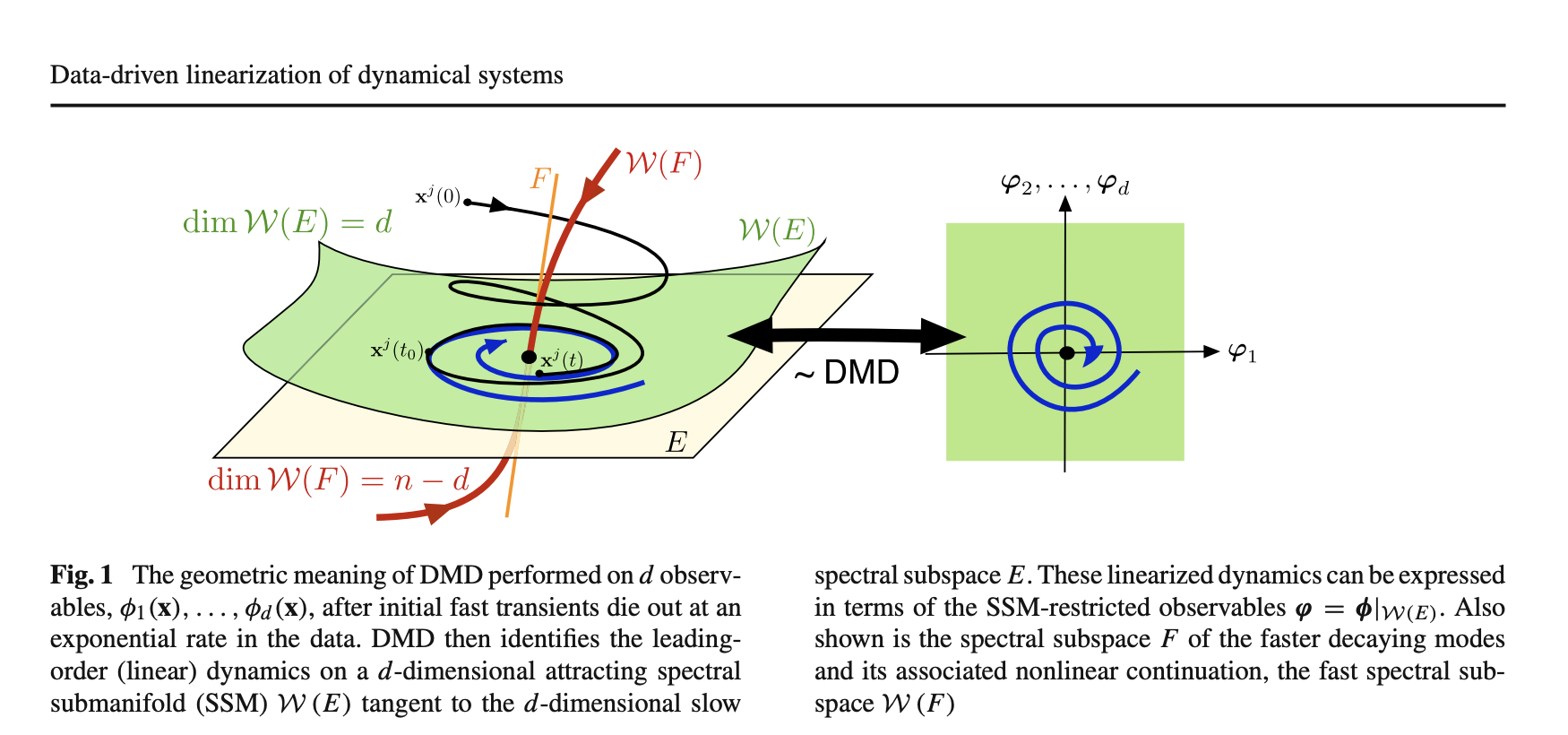
Новый подход: Data-Driven Linearization (DDL)
Для преодоления этих ограничений исследователи представляют новую технику под названием Data-Driven Linearization (DDL). Этот метод создает линеаризующие преобразования в пределах медленных спектральных подмногообразий (SSM) динамической системы, обеспечивая, что полученные линейные модели точно улавливают доминирующую динамику системы, не поддаваясь переобучению. Основное новшество DDL заключается в его способности выполнять линеаризации более высокого порядка, оставаясь действительным в условиях, часто встречающихся при использовании общих наблюдаемых и недегенеративных данных. Этот подход не только повышает точность моделирования, но и улучшает вычислительную эффективность, что делает его очень подходящим для сложных прикладных систем.
Преимущества DDL и его применение
Методология DDL включает разработку линеаризующих преобразований, используя свойства медленных SSM, которые представляют собой многомерные многообразия, описывающие основную динамику системы. Процесс начинается с выявления устойчивой гиперболической фиксированной точки и обеспечения недегенеративности как наблюдаемых, так и используемых матриц данных. Затем формулируется функция стоимости для балансировки ошибки инвариантности по наблюдаемым траекториям с ошибкой, возникающей из обратного преобразования. Эта функция стоимости минимизируется с использованием итерационных оптимизационных алгоритмов, таких как метод Левенберга-Марквардта или методы градиентного спуска. Фокусируясь на наиболее влиятельной динамике и уменьшая сложность модели, DDL достигает более надежного и точного представления исходной нелинейной системы по сравнению с традиционными методами.
Обширные оценки через числовые симуляции и анализ экспериментальных данных показывают, что метод DDL значительно превосходит существующие методы, такие как DMD и EDMD. Модели, разработанные с использованием DDL, обладают более низкими ошибками прогнозирования и требуют меньше времени для вычислений, что указывает на более эффективное и точное улавливание динамики системы. Эти улучшения являются последовательными для различных эталонов и тестовых случаев, подчеркивая универсальность и эффективность метода в обработке широкого спектра нелинейных динамических систем. Превосходная производительность DDL подчеркивает его потенциал как мощного инструмента для исследователей и инженеров, стремящихся к точным и эффективным моделям.
Заключение и перспективы
Метод Data-Driven Linearization представляет собой существенное достижение в моделировании нелинейных динамических систем, решая основные проблемы, связанные с традиционными методами линеаризации. Используя динамику в медленных спектральных подмногообразиях и применяя стратегии линеаризации более высокого порядка, этот подход создает модели, которые одновременно точны и вычислительно эффективны. Успех DDL в различных оценках свидетельствует о его широких возможностях и потенциале улучшить прогностическое моделирование, проектирование систем управления и точность моделирования во многих научных и инженерных областях. Это новшество открывает путь к более надежному и эффективному анализу сложных систем, внося значительный вклад в область моделирования динамических систем и искусственного интеллекта.
Подробнее о статье можно узнать здесь.
«`


















