«`html
Революционное доказательство теорем: как синтетические доказательства преобразуют возможности LLM
Доказательные ассистенты, такие как Lean, обеспечивают высокую точность математических доказательств, решая проблему возрастающей сложности современной математики, которая часто приводит к ошибкам. Формальные языки, такие как Lean, Isabelle и Coq, создают компьютер-проверяемые доказательства, но требуют значительных усилий и экспертизы. Автоматизированное доказательство теорем становится все более важным, с новыми методами, сосредоточенными на алгоритмах поиска потенциальных решений.
Практические решения и ценность
Исследователи разработали метод для генерации обширных данных LFourfour proof из задач математических соревнований школьников и студентов. Путем перевода этих задач в формальные утверждения, фильтрации низкокачественных и генерации доказательств, был создан набор данных из 8 миллионов утверждений. Путем настройки модели DeepSeekMath 7B на этих данных была достигнута точность в 46.3% в генерации полного доказательства на тесте Lean 4 miniF2F, превышающая результаты GPT-4. Их модель также решала 5 из 148 задач бенчмарка FIMO, превосходя GPT-4.
Автоматизированное доказательство теорем является ключевой областью исследований в области искусственного интеллекта. Недавние прорывы в глубоком обучении и модельно-управляемом поиске оживили автоматизированное доказательство теорем, объединяя нейронные модели с алгоритмами поиска и обучения с подкреплением. Эти методы, хотя и мощные, требуют больших ресурсов. Автоформализация, преобразование естественного языка в формальные утверждения, решает проблему ограниченных обучающих данных. Недавние усилия синтезировать большие наборы формальных доказательств с использованием LLM значительно улучшают производительность нейронных доказательств на сложных математических задачах.
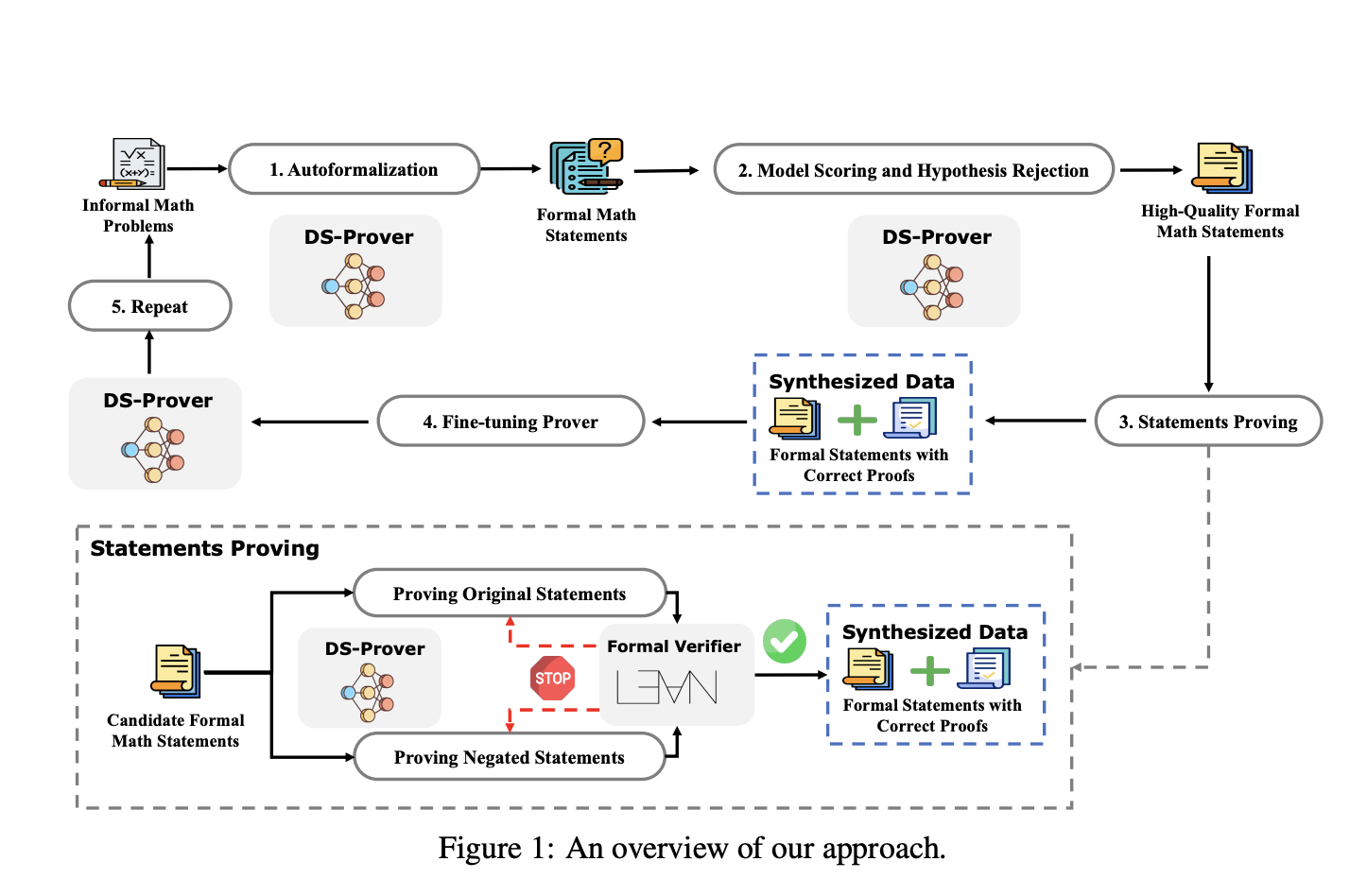
Подход включает четыре основных этапа. Формальные математические утверждения изначально генерируются из большой коллекции неформальных математических задач. Эти автоформализованные утверждения проходят фильтрацию через оценку модели и отклонение гипотез для выбора качественных. Модель DeepSeek-Prover затем пытается доказать эти утверждения с проверкой корректности формальным верификатором Lean 4, что приводит к проверенным формальным утверждениям и доказательствам. Эти данные используются для настройки модели DeepSeek-Prover, и процесс повторяется до тех пор, пока улучшения не становятся незначительными. Для повышения эффективности доказательства одновременно доказываются и исходные утверждения и их отрицания, быстро отбрасывая недопустимые утверждения.
DeepSeek-Prover, основанный на модели DeepSeekMath-Base 7B, был настроен с глобальным размером пакета 512 и постоянной скоростью обучения 1 × 10^−4, включая 6 000 шагов разогрева с использованием синтетических данных. Его производительность была сравнена с GPT-3.5, GPT-4 и несколькими продвинутыми методами. Оценки на бенчмарках miniF2F и FIMO показали, что DeepSeek-Prover превзошел другие методы, достигнув 60.2% на miniF2F-valid и 52.0% на miniF2F-test, значительно превышая результаты GPT-4. Бенчмарк FIMO успешно доказал пять теорем с разными попытками, превзойдя GPT-4, который не смог установить ни одной.
В заключение, исследование разработало метод для генерации обширных синтетических доказательств из задач математических соревнований школьников и студентов. Путем перевода проблем естественного языка в формальные утверждения, фильтрации низкокачественных данных и использования итеративного доказательства было создано 8 миллионов точек данных, значительно улучшающих производительность модели DeepSeekMath 7B в автоматизированном доказательстве теорем. Модель превосходит GPT-4 и другие методы бенчмарков, такие как miniF2F и FIMO. Открытые данные и модель направлены на продвижение исследований в области автоматизированного доказательства теорем и улучшение возможностей больших языковых моделей в формальном математическом рассуждении, с планами расширения охвата рассматриваемых математических проблем в будущей работе.
Проверьте Статью. Вся заслуга за это исследование принадлежит его ученым. Также не забудьте подписаться на нас в Twitter. Присоединяйтесь к нашему каналу в Telegram, Discord и группе в LinkedIn.
Если вам нравится наша работа, вам понравится наш новостной бюллетень.
Не забудьте присоединиться к нашему сообществу в SubReddit с более чем 42 тысячами участников.
«`



















